列联表分析

	发生	未发生	合计
对照组	a	b	\(N_0\)
试验组	c	d	\(N_1\)

率比（Risk Ratio），也称相对危险度（Relative Risk）: \(RR=\frac{a/N_0}{c/N_1}\)，相对量，这里表示对照组发生事件是试验组发生事件的多少倍。

率差（Rate Difference）: \(RD=\frac{a}{N_0}-\frac{c}{N_1}\)，绝对量，率差能够直观的看出疗效的大小，可理解为试验组比对照组多百分之多少的可能发生事件。

优势比，也称比值比（Odds Ratio）:\(OR=\frac{a/b}{c/d}\)，这里反映了组别之间发生事件的关联强度。

率差

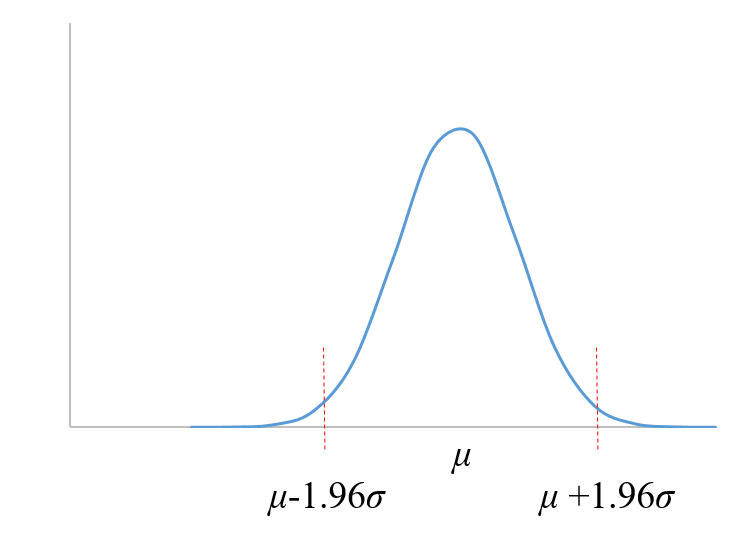
假设样本均值等于总体均值，其置信区间以均值为中心分布在其两侧。方法：正态近似法。

data test1;
    gp="A";r=0;n=13;output;
    gp="A";r=1;n=48;output;
    gp="B";r=0;n=8;output;
    gp="B";r=1;n=56;output;
run;


**** Method 1 ****;
proc freq data=test1;
    tables gp*r/ riskdiff(cl=exact);
    exact riskdiff;
    weight n/ zeros;
run;

假设样本均值不等于总体均值，样本出现在总体分布的置信区间内。方法：Miettinen and Nurminen.

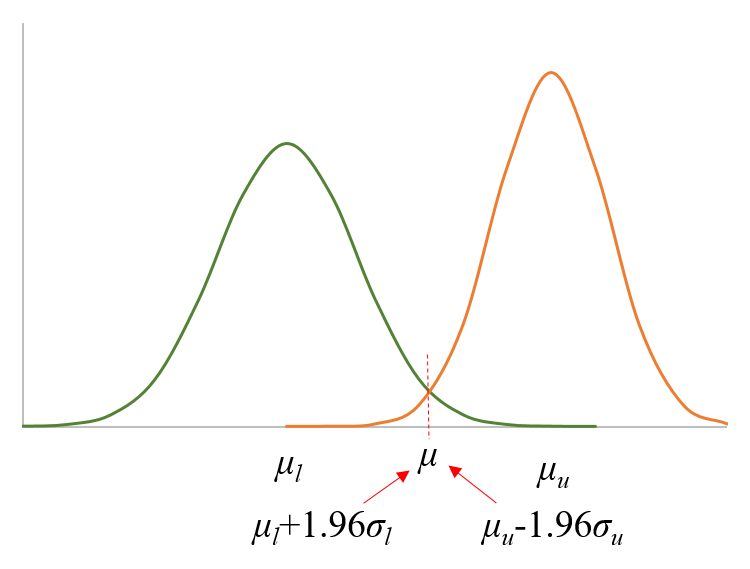
试验组与对照组的比率不是都为100%或0%（MN方法）

data test1;
    gp="A";r=0;n=13;output;
    gp="A";r=1;n=48;output;
    gp="B";r=0;n=8;output;
    gp="B";r=1;n=56;output;
run;


**** Method 1 ****;
proc freq data=test1;
    tables gp*r/ riskdiff(cl=mn);
    weight n/ zeros;
    ods output pdiffcls=mn;
run;

试验组与对照组的比率都为100%或0%（MN方法）

%macro ratediff(n1=,n1_event=,n2=,n2_event=,alpha=,side=);
data mienur;
n1=&n1.;
a1=&n1_event.;
a2=n1-a1;
p1=a1/n1;
n2=&n2.;
a3=&n2_event.;
a4=n2-a3;
p2=a3/n2;
z=probit(1-&alpha./&side.);
d=p1-p2;
**率差置信区间下限;
**率差置信区间上限;
l_diff=-(z**2*(a1+a3)/((a1+a3-1)*a1))/((z**2*(a1+a3)/((a1+a3-1)*a1))+1);
u_diff= (z**2*(a1+a3)/((a1+a3-1)*a3))/((z**2*(a1+a3)/((a1+a3-1)*a3))+1);
run;
%mend ratediff;

%ratediff(n1=100,n1_event=100,n2=100,n2_event=100,alpha=0.05,side=2);

分层的Miettinen-Nurminen方法计算率差与P值

%macro rrv(c0,c1,s0,s1,z,rd,ra,rb,vv);/*根据rd计算r0和r1*/
 c0=&c0.;
 c1=&c1.;
 s0=&s0.;
 s1=&s1.;
 c=c1+c0;
 s=s1+s0;
 p1=c1/s1;
 p0=c0/s0;
 z2=&z.**2;
 rd=&rd.;

 l3=s;
 l2=(s1+2*s0)*rd-s-c;
 l1=(s0*rd-s-2*c0)*rd+c;
 l0=c0*rd*(1-rd);

 q=l2**3/(3*l3)**3-l1*l2/(6*l3**2)+l0/(2*l3);
 p=sign(q)*(l2**2/(3*l3)**2-l1/(3*l3))**0.5;
 if p=0 then aa=0; 
 else aa=q/p**3;
 if abs(aa)>1 then aa=1;
 a=1/3*(pi+arcos(aa));
 r0=2*p*cos(a)-l2/(3*l3);

 r1=r0+rd;
 v=(r1*(1-r1)/s1+r0*(1-r0)/s0)*s/(s-1);
 &ra.=r0;
 &rb.=r1;
 &vv.=v;
%mend;

%macro stra_mn(dat=,stra=,trt=,c=,n=,alp=,Wmethod=2,all=0,out=);

%if &stra.=0 %then %do;

proc sort data=&dat. out=dat1;
 by &trt.;
run;

data dat1x;
 set dat1 nobs=nob;
 by &trt.;
 array ccc(2);
 array nnn(2);
 retain ccc: nnn:;
 if first.&trt. then do;
    i+1;
    ccc(i)=&c.;
    nnn(i)=&n.;
 end;
 if _N_=nob then do;
    ca=ccc(1);
    cb=ccc(2);
    na=nnn(1);
    nb=nnn(2);
    output;
 end;
 keep ca cb na nb;
run;

data dat2;
 set dat1x;
 z=probit(1-&alp./2);
 pi=constant("pi");
 pa=ca/na;
 pb=cb/nb;

/*计算置信下限*/

 str=0;
 qxq=0;
 do qcyc=1 to 3;

    poit=10**(-qcyc*2);
    lmin=10;
    str=str+qxq*poit*100;

 do cyc=-99 to 99;
    rdlx=str+cyc*poit;
    %rrv(ca,cb,na,nb,z,rdlx,ra,rb,vv);
    if abs(vv)<10**(-12) then vv=0;
    rdx=pb-pa-(z*z*vv)**0.5; /*置信下限*/
    if vv^=0 then diff=abs(rdx-rdlx);
    if diff<lmin then do;
       lmin=diff;
       qxq=cyc;
    end;
    if &all.=1 then output;
 end; 

 end;
 rdl=str+qxq*poit;

 /*计算置信上限*/
 str=0;
 qxq=0;
 do qcyc=1 to 3;

    poit=10**(-qcyc*2);
    dmin=10;
    str=str+qxq*poit*100;

 do cyc=-99 to 99;
    rdlx=str+cyc*poit;
    %rrv(ca,cb,na,nb,z,rdlx,ra,rb,vv);
    if abs(vv)<10**(-12) then vv=0;
    rdx=pb-pa+(z*z*vv)**0.5; /*置信上限*/
    if vv^=0 then diff=abs(rdx-rdlx);
    if diff<dmin then do;
       dmin=diff;
       qxq=cyc;
    end;
    if &all.=1 then output;
 end; 

 end;
 rdu=str+qxq*poit;
 
/*Z统计量*/

 rdlx=0;
 %rrv(ca,cb,na,nb,z,rdlx,ra,rb,vv);
 if abs(vv)<10**(-16) then Zsc=0;
 else Zsc=-abs((pb-pa)/vv**0.5);
 Pvalue=probnorm(Zsc)*2;

 /*率差*/
 rankdiff=pb-pa;
 output;

 %if &all.=1 %then %do;
     keep diff rdx rdlx rdl ra rb vv rdl dmin rdu lmin str qxq;
 %end;
 %else %do;
     keep rdl rdu dmin lmin Zsc Pvalue rankdiff ;
 %end;
run;

%end;



/**************************************************/
/*分层MN*/
%else %do;

proc sort data=&dat. out=dat1;
 by &stra. &trt.;
run;

data _NULL_;
 set dat1 nobs=nob;
 array cc(99);
 array nn(99);
 retain cc: nn:;
 by &stra. &trt.;
 x+1;
 cc(x)=&c.;
 nn(x)=&n.;
 if _N_=nob then do;
    grp=x/2;
    do i=1 to grp;
       call symputx("c"||strip(put(i,best.))||"_0",strip(put(cc(i*2-1),best.)));
       call symputx("c"||strip(put(i,best.))||"_1",strip(put(cc(i*2),best.)));
       call symputx("n"||strip(put(i,best.))||"_0",strip(put(nn(i*2-1),best.)));
       call symputx("n"||strip(put(i,best.))||"_1",strip(put(nn(i*2),best.)));
    end;
    call symputx("Ntrt",strip(put(x/2,best.)));
 end;
run;

data dat2;
 array ca(&Ntrt.);
 array cb(&Ntrt.);
 array na(&Ntrt.);
 array nb(&Ntrt.);
 array pa(&Ntrt.);
 array pb(&Ntrt.);
 array ra(&Ntrt.);
 array rb(&Ntrt.);
 array vv(&Ntrt.);
 array wfr(&Ntrt.);
 array sw(&Ntrt.);
 ntrt=&Ntrt.;
 %do i=1 %to &Ntrt.;
     ca&i.=&&c&i._0.;
     cb&i.=&&c&i._1.;
     na&i.=&&n&i._0.;
     nb&i.=&&n&i._1.;
 %end;
 z=probit(1-&alp./2);
 pi=constant("pi");
 do i=1 to ntrt;
    pa(i)=ca(i)/na(i);
    pb(i)=cb(i)/nb(i);
 end;

 /*率差*/
 ew=0;
 do i=1 to ntrt;  
    %if &wmethod.=1 %then %do; 
        wfr(i)=(na(i)+nb(i));
    %end;
    %if &wmethod.=2 %then %do; 
        wfr(i)=1/(1/na(i)+1/nb(i));
    %end;
    ew=ew+wfr(i);
 end;
 rra=0;
 rrb=0;
 do i=1 to ntrt;
    sw(i)=wfr(i)/ew;
    rra=rra+sw(i)*pa(i);
    rrb=rrb+sw(i)*pb(i);
 end;
 rankdiff=rrb-rra;

 /*计算置信下限*/
 str=0;
 qxq=0;
 do qcyc=1 to 3;

    poit=10**(-qcyc*2);
    lmin=10;
    str=str+qxq*poit*100;

 do cyc=-99 to 99;
    rdlx=str+cyc*poit;
  
    do i=1 to ntrt;
       %rrv(ca(i),cb(i),na(i),nb(i),z,rdlx,ra(i),rb(i),vv(i));
       if abs(vv(i))<10**(-12) then vv(i)=0;
    end;

    rra=0;
    rrb=0;
    vxv=0;
    do i=1 to ntrt;
       rra=rra+sw(i)*pa(i);
       rrb=rrb+sw(i)*pb(i);
       vxv=vxv+vv(i)*sw(i)*sw(i);
    end;
    rdx=rrb-rra-(z*z*vxv)**0.5; /*置信下限*/
    diff=abs(rdx-rdlx);
    if diff<lmin then do;
       lmin=diff;
       qxq=cyc;
    end;
    if &all.=1 then output;
 end; 

 end;

 rdl=str+qxq*poit;


 /*计算置信上限*/
 str=0;
 qxq=0;
 do qcyc=1 to 3;

    poit=10**(-qcyc*2);
    dmin=10;
    str=str+qxq*poit*100;

 do cyc=-99 to 99;
    rdlx=str+cyc*poit;
  
    do i=1 to ntrt;
       %rrv(ca(i),cb(i),na(i),nb(i),z,rdlx,ra(i),rb(i),vv(i));
       if abs(vv(i))<10**(-12) then vv(i)=0;
    end;

    rra=0;
    rrb=0;
    vxv=0;
    do i=1 to ntrt;
       rra=rra+sw(i)*pa(i);
       rrb=rrb+sw(i)*pb(i);
       vxv=vxv+vv(i)*sw(i)*sw(i);
    end;
    rdx=rrb-rra+(z*z*vxv)**0.5; /*置信上限*/
    diff=abs(rdx-rdlx);
    if diff<dmin then do;
       dmin=diff;
       qxq=cyc;
    end;
    if &all.=1 then output;
 end; 

 end;

 rdu=str+qxq*poit;
 
/*Z统计量*/

 rdlx=0;
  
 do i=1 to ntrt;
    %rrv(ca(i),cb(i),na(i),nb(i),z,rdlx,ra(i),rb(i),vv(i));
    if abs(vv(i))<10**(-12) then vv(i)=0;
 end;

 rra=0;
 rrb=0;
 vxv=0;
 do i=1 to ntrt;
    rra=rra+sw(i)*pa(i);
    rrb=rrb+sw(i)*pb(i);
    vxv=vxv+vv(i)*sw(i)*sw(i);
 end;
 Zsc=-abs((rrb-rra)/vxv**0.5);
 Pvalue=probnorm(Zsc)*2;

 output;


 %if &all.=1 %then %do;
     keep diff rdx rdlx rdl rra rrb vxv ra: rb: rdl dmin;
 %end;
 %else %do;
     keep rdl rdu dmin lmin Zsc Pvalue rankdiff ;
 %end;
run;

%end;

data &out.;
 set dat2;
 RateDiff=rankdiff;
 LowerCL=rdl;
 UpperCL=rdu;
 Z=Zsc;
 P=Pvalue;
 keep ratediff LowerCL UpperCL Z P;
run;

%mend;


/*dat:输入的数据集文件名,stra:分层因素,trt:分组变量名,c:事件数的变量名,n:样本量的变量名,每一层的n都不能为0*/
/*Wmethod为权重计算方法,本次分析使用Wmethod=2*/
/*Wmethod=1: Wi=n0i+n1i*/
/*Wmethod=2: Wi=1/(1/n0i+1/n1i)*/

/*当stra设为0时,为不分层的MN方法,但优先推荐使用SAS自带的procedure计算不分层的MN方法*/

逆方差法（Inverse Variance Method）计算率差及其置信区间

/* 创建原始数据集 */
data studies;
    input study $ age_group $ n_treatment success_treatment n_control success_control;
    datalines;
1 30-40 100 45 100 30
2 40-50 80 50 90 40
3 30-40 150 75 150 60
4 40-50 120 70 130 55
;
run;

/* 计算各组的比例差及其标准误 */
data effect_sizes;
    set studies;

    /* 计算治疗组和对照组的成功率 */
    p_treatment = success_treatment / n_treatment;
    p_control = success_control / n_control;

    /* 计算比例差 */
    prop_diff = p_treatment - p_control;

    /* 计算标准误 */
    se_prop_diff = sqrt((p_treatment * (1 - p_treatment) / n_treatment) + 
                         (p_control * (1 - p_control) / n_control));

    output; /* 输出每个研究的效应量和标准误 */
run;

/* 计算每个分层组的权重（逆方差法） */
data weighted_effects;
    set effect_sizes;
    weight = 1 / (se_prop_diff**2); /* 逆方差法 */
run;

/* 合成总体效应量 */
proc sql;
    select 
        sum(weight * prop_diff) / sum(weight) as combined_prop_diff,
        sqrt(1 / sum(weight)) as combined_se
    into :combined_diff, :combined_se
    from weighted_effects;
quit;

/* 计算95%置信区间 */
data confidence_interval;
    lower_bound = &combined_diff - 1.96 * &combined_se; /* 正常置信区间计算 */
    upper_bound = &combined_diff + 1.96 * &combined_se;
    combined_proportion_difference = &combined_diff;
run;

data weightd_q;
    set weighted_effects;
    qdiff = weight * (prop_diff - &combined_diff.)**2;
run;

proc sql noprint;
    select sum(qdiff) into: combined_q from weightd_q;
quit;


/* 计算P值 - 使用卡方检验 */
data p_value;
    Q = &combined_q; 
    p_value = 1 - probchi(Q, 3); /* 双尾P值计算 */
run;

R语言计算RD, OR, RR

R语言sasLM package（https://cran.r-project.org/web/packages/sasLM/sasLM.pdf）可以用于计算率差（RD），率比（RR），优势比（OR）

library(sasLM)

###计算几何均值
geoMean(mtcars$mpg)
geoCV(mtcars$mpg)

###无连续性校正
RD(y1=55,
   n1=67,
   y2=43,
   n2=51)

###分层的MN方法计算率差
y1 <- c(10, 12)
n1 <- c(30, 50)
y2 <- c(43, 55)
n2 <- c(90, 80)
d0 <- data.frame(y1, n1, y2, n2)
RDmn(d0, conf.level = 0.95)

###没有分层的MN方法计算率差
RDmn1(y1=55,
   n1=67,
   y2=43,
   n2=51)

###逆方差法（inverse variance method）计算率差
RDinv(d0, conf.level = 0.95)